Đề cương ôn tập học kì I môn Toán Lớp 9 - Năm học 2014-2015 - Trường THCS Hùng Thắng

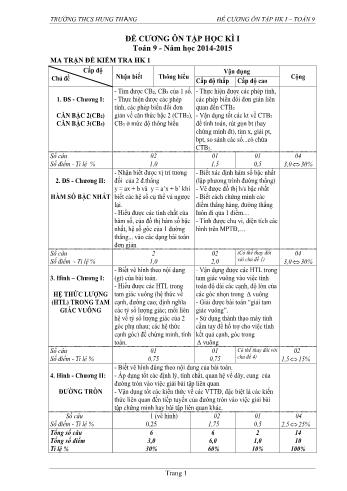
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 1 
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I 
Toán 9 - Năm học 2014-2015 
MA TRẬN ĐỀ KIỂM TRA HK 1 
 Cấp độ 
 Chủ đề Nhận biết Thông hiểu 
Vận dụng 
Cộng 
Cấp độ thấp Cấp độ cao 
1. ĐS - Chương I: 
CĂN BẬC 2(CB2) 
CĂN BẬC 3(CB3) 
- Tìm được CB2, CB3 của 1 số. 
- Thực hiện được các phép 
tính, các phép biến đổi đơn 
giản về căn thức bậc 2 (CTB2), 
CB3 ở mức độ thông hiểu 
- Thực hiện được các phép tính, 
các phép biến đổi đơn giản liên 
quan đến CTB2 
- Vận dụng tốt các kt về CTB2 
để tính toán, rút gọn bt (hay 
chứng minh đt), tìm x, giải pt, 
bpt, so sánh các số...có chứa 
CTB2. 
Số câu 
Số điểm - Tỉ lệ % 
02 
1,0 
01 
1,5 
01 
0,5 
04 
3,0 30% 
2. ĐS - Chương II: 
HÀM SỐ BẬC NHẤT 
- Nhận biết được vị trí tương 
đối của 2 đ.thẳng 
y = ax + b và y = a’x + b’ khi 
biết các hệ số cụ thể và ngược 
lại. 
- Hiểu được các tính chất của 
hàm số, của đồ thị hàm số bậc 
nhất, hệ số góc của 1 đường 
thẳng... vào các dạng bài toán 
đơn giản 
- Biết xác định hàm số bậc nhất 
(lập phương trình đường thẳng) 
- Vẽ được đồ thị h/s bậc nhất 
- Biết cách chứng minh các 
điểm thẳng hàng, đường thẳng 
luôn đi qua 1 điểm.... 
- Tính được chu vi, diện tích các 
hình trên MPTĐ, 
Số câu 
Số điểm - Tỉ lệ % 
2 
1,0 
02 
2,0 
(Có thể thay đổi 
với chủ đề 1) 
04 
3,0 30% 
3. Hình – Chương I: 
HỆ THỨC LƯỢNG 
(HTL) TRONG TAM 
GIÁC VUÔNG 
- Biết vẽ hình theo nội dung 
(gt) của bài toán. 
- Hiểu được các HTL trong 
tam giác vuông (hệ thức về 
cạnh, đường cao; định nghĩa 
các tỷ số lượng giác; mối liên 
hệ về tỷ số lượng giác của 2 
góc phụ nhau; các hệ thức 
cạnh góc) để chứng minh, tính 
toán. 
- Vận dụng được các HTL trong 
tam giác vuông vào việc tính 
toán độ dài các cạnh, độ lớn của 
các góc nhọn trong vuông 
- Giải được bài toán “giải tam 
giác vuông”. 
- Sử dụng thành thạo máy tính 
cầm tay để hổ trợ cho việc tính 
kết quả cạnh, góc trong 
 vuông 
Số câu 
Số điểm - Tỉ lệ % 
01 
0,75 
01 
0,75 
Có thể thay đổi với 
chủ đề 4) 
 02 
1,5 15% 
4. Hình - Chương II: 
ĐƯỜNG TRÒN 
- Biết vẽ hình đúng theo nội dung của bài toán. 
- Áp dụng tốt các định lý, tính chất, quan hệ về dây, cung của 
đường tròn vào việc giải bài tập liên quan 
- Vận dụng tốt các kiến thức về các VTTĐ, đặc biệt là các kiến 
thức liên quan đến tiếp tuyến của đường tròn vào việc giải bài 
tập chứng minh hay bài tập liên quan khác. 
 Số câu 
Số điểm - Tỉ lệ % 
 1 (vẽ hình) 
0,25 
 02 
 1,75 
01 
0,5 
 04 
2,5 25% 
Tổng số câu 
Tổng số điểm 
Tỉ lệ % 
6 
3,0 
30% 
6 
6,0 
 60% 
2 
1,0 
10% 
14 
10 
100% 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 2 
A - LÝ THUYẾT 
I. ĐẠI SỐ 
1. A xác định khi A ≥ 0 
2. Các công thức biến đổi căn thức 
2
A 0A A 2A A
A
A neáu A 0
 neáu A 0
 .AB A B (A 0, B 0) 
A A
B B
 (A 0, B > 0) 
 2A B A B (B 0) 
 2A B A B (A 0, B 0) 2A B A B (A < 0, B 0) 
A 1
AB
B B
 (AB 0, B 0) 
A A B
BB
 (B > 0) 
 C A BC
A BA B
(A, B 0, A B) 
2
C A BC
A BA B
 (A 0, A B2) 
3
3 33 AA A 3 33 .B .A A B 
3
3
3
B 0
B
A A
B
3. Rút gọn biểu thức chứa căn dạng: M 2 N , M 0, N 0 
 Cách giải: Tìm A và B sao cho: 
A B M
A.B N
 , với A và B là 2 nghiệm của phương 
trình bậc hai: x2 – Mx + N = 0. Khi đó: 
2
M 2 N (A B) 2 A.B A B A B 
4. Tính chất so sánh các căn thức 
 a b a b a 0, b 0 
 3 3a b a b 
5. Phương trình và bất phương trình chứa căn thức 
   
2 f (x) a
f (x) a a 0 f (x) a
f (x) a
 2f (x) a a 0 f (x) a 
 2f (x) a a 0 f (x) a 
2
f (x) 0
f (x) a a 0
f (x) a
 
2
g(x) 0
f (x) g(x)
f (x) g(x)
f (x) 0
f (x) g(x) g(x) 0
f (x) g(x)
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 3 
6. Định nghĩa, tính chất hàm số bậc nhất 
a) Hàm số bậc nhất là hàm số có dạng y = ax + b (a 0) 
b) Hàm số bậc nhất xác định với mọi giá trị x . 
 + Hàm số đồng biến trên khi a > 0. 
+ Nghịch biến trên khi a < 0. 
7. Đồ thị của hàm số y = ax + b (a 0) có a là hệ số góc và b là tung độ gốc. 
 + Nếu đồ thị hàm số cắt trục tung tại điểm có tung độ là y0 thì y0 = b 
 + Nếu đồ thị hàm số cắt trục hoành tại điểm có hoành độ là x0 thì 0
b
x
a
+ Nếu đồ thị hàm số đi qua gốc tọa độ thì y = ax. 
 + Gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox 
 Nếu a > 0 thì là góc nhọn và tan = a 
 Nếu a < 0 thì là góc tù và tan(1800 – ) = |a|. 
8. Cho (d): y = ax + b (a ≠ 0) và (d'): y = a'x + b' (a’ ≠ 0) 
 (d)  (d') 
a a '
b b '
 (d)  (d') a a' 
 (d)  (d')
a a '
b b '
 (d)  (d') a.a ' 1 
 (D) cắt (D’) tại 1 điểm trên trục tung 
a a '
b b '
 (D) cắt (D’) tại 1 điểm trên trục hoành 
a a '
b b '
a a '
II. HÌNH HỌC 
1. Các hệ thức về cạnh và đường cao trong tam giác vuông 
 Cho ABC vuông tại A, đường cao AH. Ta có: 
 b2 = a.b’ c2 = a.c’ 
 h2 = b’. c’ 
 a.h = b.c 
2 2 2
1 1 1
h b c
 a2 = b2 + c2 (Định lí Py-ta-go) 
2. Tỉ số lượng giác của góc nhọn 
a) Định nghĩa: 
sin
tan t
caïnh ñoái caïnh keà
cos
caïnh huyeàn caïnh huyeàn
caïnh ñoái caïnh keà
co
caïnh keà caïnh ñoái
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 4 
b) Tính chất: 
+ Cho hai góc và  phụ nhau. Khi đó: 
 sin = cos  cos = sin  
 tan = cot  cot = tan  
+ Cho góc nhọn . Ta có: 
 0 < sin < 1 0 < cos < 1 
 tan = 
sin
cos
 cot = 
cos
sin
 sin2 + cos2 = 1 tan .cot = 1 
+ Cho và  là các góc nhọn. Nếu <  thì 
sin sin , tan tan
cos cos , cot cot
   
   
3. Đường tròn 
a) Đường tròn ngoại tiếp tam giác là đường tròn đi qua 3 đỉnh của tam giác, có tâm là 
giao điểm của ba đường trung trực của tam giác đó. 
b) Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, có tâm 
là giao điểm của ba đường phân giác của tam giác đó. 
c) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền. 
d) Nếu một tam giác nội tiếp đường tròn có một cạnh là đường kính thì tam giác đó là 
tam giác vuông. 
e) Trong một đường tròn, dây lớn nhất là đường kính. 
f) Định lí về quan hệ vuông góc giữa đường kính và dây cung: 
 + Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của 
dây ấy. 
 + Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy. 
g) Các tính chất của tiếp tuyến: 
 + Nếu một đường thẳng là một tiếp tuyến của một đường tròn thì nó vuông góc với bán 
kính đi qua tiếp điểm. 
 + Nếu một đường thẳng vuông góc với bán kính tại một điểm nằm trên đường tròn thì 
đường thẳng đó là một tiếp tuyến của đường tròn. 
+ Nếu 2 tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: 
- Điểm đó cách đều hai tiếp điểm 
- Tia kẻ từ điểm đó đi qua tâm đường tròn là tia phân giác của góc tạo bởi hai tiếp 
tuyến. 
- Tia kẻ từ tâm đường tròn đi qua điểm đó là tia phân giác của góc tạo bởi hai bán 
kính đi qua các tiếp điểm. 
 h) Định lí liên hệ giữa dây và khoảng cách đến tâm: Trong một đường tròn 
 + Nếu hai dây bằng nhau thì khoảng cách từ tâm đến hai dây đó bằng nhau và ngược lại. 
 + Nếu dây nào lớn hơn thì khoảng cách từ tâm đến dây đó nhỏ hơn và ngược lại. 
 i) Vị trí tương đối của đường thẳng và đường tròn: SGK/109 
 j) Vị trí tương đối của hai đường tròn: SGK/121 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 5 
B - BÀI TẬP 
I. CĂN BẬC HAI – CĂN BẬC BA 
Bài 1. Rút gọn các biểu thức sau: 
1) 
2 213 12 2) 
128
2 
3) 160. 8,1 4) 
23 33 5 . 3 5 64 27 3 
5) 
22(2 3) 2 6) 2 2(4 15) ( 15 3) 
7) 2 2(3 2 2) ( 8 4) 8) 45 20 80 : 5 
9) 
3
6 128 50 7 8 :3 2
5
 10) 
16 1
2 27 48 8
3 3
11) 
3 4
2 48 27 2 3
2 3
  
 12) 125 12 2 5 3 5 3 27 
13) 
2 2
11 3 11 3
 14) 
1 1
5 3 5 3
15) 
10 2 2 2
5 1 2 1
 16) 
5 5 5 5
1 1
1 5 1 5
17) 8 2 15 18) 15 6 6 15 6 6 
Bài 2. Rút gọn biểu thức: 
a a a 2 a 1
A 1 2
a 1 a 1
 với a 0; a 1 
Bài 3. Cho biểu thức 
x
A x 2 x 1
9
 ( x 0 ) 
 a) Rút gọn biểu thức A b) Tính giá trị A với 
1
x 2
4
Bài 4. Cho biểu thức 2B 3 2x 1 4x 4x 
 a) Rút gọn B b) Tính giá trị B khi x 2010 
Bài 5. Cho biểu thức 
x 2 x 1
E
x 1 x x 1
 (x > 0, x ≠ 1) 
 a) Rút gọn E b) Tìm x để E > 0 
Bài 6. Cho biểu thức x 1 2 xG x 1
x 1x 1 1 x
  
(x > 0, x ≠ 1) 
 a) Rút gọn biểu thức G b) Tìm x để G 2 
Bài 7. Giải phương trình: 
a) x 5 3 b) 4 5x 12 
c) 
2x 6x 9 3 d) 
2216 24x 9x 5 
e) 
1
4x 20 x 5 9x 45 4
3
x 3
f ) 4x 12 3 2
9
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 6 
II. HÀM SỐ VÀ ĐỒ THỊ 
Bài 1. Cho hai đường thẳng (d): y = 4 – 2x và (d’): y = 3x + 1 
 a) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ. 
 b) Gọi N là giao điểm của hai đường thẳng (d) và (d’). Tìm tọa độ của điểm N. 
 c) Tính số đo góc tạo bởi đường thẳng (d’) với trục Ox 
Bài 2. Cho hai hàm số y = 0,5 x + 2 (d1) và y = -2x +5 (d2) 
a) Vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ. 
 b) Tính góc tạo bởi đường thẳng (d1) với trục Ox. 
c) Gọi giao điểm của các đường thẳng (d1) và (d2) với trục Ox theo thứ tự là A và 
B, giao điểm của (d1) và (d2) là C. Tìm tọa độ điểm A, B, C. 
 d) Tính chu vi và diện tích ABC. Tính các góc của tam giác ABC. 
Bài 3. Cho 2 đường thẳng (d1): y = kx + m + 3 (k ≠ 0) và (d2): y = (2 – k)x + 5 – m (k ≠2). 
Với giá trị nào của k và m thì (d1) và (d2) : 
a) Cắt nhau b) Song song với nhau c) Trùng nhau 
Bài 4. Với những giá trị nào của m thì các hàm số y = 2x + m + 3 và y = 3x + 5 – m cắt 
nhau tại một điểm trên trục tung. 
Bài 5. Tìm m để hai đường thẳng y = 2x – 3 và y = 3x – m + 5 cắt nhau tại một điểm 
 a) nằm trên trục hoành b) có hoành độ bằng 3 
Bài 6. Cho hàm số y m 1 x m m 1 
 a) Tìm m để hàm số đồng biến trên . 
 b) Tìm m để đồ thị hàm số đi qua điểm 
1
A ; 2
2
. Vẽ đồ thị hàm số với m tìm được. 
 c) Tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng x 2y 0 . 
Bài 7. Cho hàm số y 1 2m x m 1 (d) 
 a) Tìm m để hàm số nghịch biến trên . 
b) Xác định m để đường thẳng (d) đi qua gốc tọa độ. 
 c) Tìm m để đường thẳng (d) đi qua A(3; 4).Vẽ đồ thị với m vừa tìm được. 
 d) Tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng (d’): y 2x 4 
 e) Tính số đo góc tạo bởi đường thẳng (d’) với trục Ox. 
Bài 8. Cho đường thẳng y = (1 – m)x + m – 2 (d). Với giá trị nào của m thì 
a) (d) đi qua điểm A(2;1)? 
b) (d) song song với đường thẳng y = 3x – 1? 
c) (d) cắt trục tung tại điểm có tung độ bằng 3? 
d) (d) cắt trục hoành tại điểm có hoành độ bằng 2? 
e) (d) vuông góc với đường thẳng y = – 2x +2013 
f) (d) tạo với trục Ox một góc nhọn? Góc tù? Góc 300? Góc 1350 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 7 
Bài 9. Viết phương trình đường thẳng thỏa mãn một trong các điều kiện sau đây: 
a) Song song với đường thẳng y = 2x – 3 và đi qua A(1;2). 
b) Đi qua điểm A(1; – 4) và có tung độ gốc bằng – 2. 
c) Đi qua điểm M(2; 3) và có hệ số góc bằng – 2. 
d) Đi qua K(1; 2) và H(– 2; 3). 
Bài 10. Xác định hàm số y = ax + b (a 0) trong các trường hợp sau: 
a) Đồ thị của hàm số là đường thẳng đi qua gốc tọa độ và có hệ số góc bằng – 2. 
b) Đồ thị của hàm số là đường thẳng cắt trục tung tại điểm có tung độ bằng – 3 và cắt 
trục hoành tại điểm có hoành độ bằng 2. 
c) Đồ thị hàm số song song song với đường thẳng y = 2 – 3x và cắt đường thẳng 
y = x + 1 tại điểm có tung độ bằng 1. 
d) Đồ thị hàm số vuông góc với đường thẳng y = 2x – 3 và cắt đường thẳng y = 2x + 1 
tại điểm có hoành độ bằng 2. 
Bài 11. Chứng minh ba đường thẳng (D1): y = x + 2; (D2): y = 2x + 1 và (D3): y = 3x đồng 
quy. 
Bài 12. Cho hai đường thẳng (d): y = x - 2 (d’): y = - 2x + 1 
a) Vẽ (d) và (d’) trên cùng một mặt phẳng toạ độ Oxy. 
b) Tìm toạ độ giao điểm C của hai đường thẳng (d) và (d’) 
c) Hãy tìm m để đường thẳng y = (m – 2)x + m và hai đường thẳng (d), (d’) đồng quy. 
Bài 13. Chứng minh 3 điểm A(0; 0,5), B(3; 4), C(– 1; – 2) thẳng hàng. 
Bài 14. 
a) Vẽ (d) y = 1 – x và (d’) 
1
y x 2
3
 trên cùng một mặt phẳng tọa độ Oxy. 
b) Gọi C là giao điểm của (d) và (d’). Tìm tọa độ của điểm C (bằng phép tính) 
c) Gọi A là giao điểm của (d) với trục tung, B là giao điểm của (d’) với trục tung. Tính 
chu vi và diện tích của tam giác ABE (với đơn vị trên các trục tọa độ là cm). 
d) Tìm m để ba điểm A, C và D(m – 1; 2) thẳng hàng. 
Bài 15. Chứng minh khi m thay đổi thì các đường thẳng sau luôn đi qua một điểm cố định. 
 a) y = (m + 4)x – m + 6 b) y = (m – 2)x – 2m + 1 
III. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 
Bài 1. Cho ABC vuông tại A, đường cao AH. 
 a) Biết AH = 12cm, CH = 5cm. Tính AC, AB, BC, BH. 
 b) Biết AB = 30cm, AH = 24cm. Tính AC, CH, BC, BH. 
 c) Biết AC = 20cm, CH = 16cm. Tính AB, AH, BC, BH. 
 d) Biết AB = 6cm, BC = 10cm. Tính AC, AH, BH, CH. 
 e) Biết BH = 9cm, CH = 16cm. Tính AC, AB, BC, AH. 
Bài 2. Cho tam giác ABC vuông tại A có 0B 60 , BC = 20cm. 
a) Tính AB, AC b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC. 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 8 
Bài 3. Giải tam giác ABC vuông tại A, biết: 
 a) AB = 6cm, 0B 40 b) AB = 10cm, 0C 35 
 c) BC = 20cm, 0B 58 d) BC = 82cm, 0C 42 
 d) BC = 32cm, AC = 20cm e) AB = 18cm, AC = 21cm 
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai, kết quả về góc làm tròn đến phút). 
Bài 4. Không sử dụng máy tính, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: 
 a) sin650; cos750; sin700; cos180; sin790 b) tan210; cot12036’; cot430; tan790. 
IV. ĐƯỜNG TRÒN 
Bài 1. Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn (O) vẽ tiếp tuyến AB (B là 
tiếp điểm). Vẽ dây BC vuông góc với OA tại H. 
a) Chứng minh rằng AC là tiếp tuyến của đường tròn (O). 
c) Khi OA = 2R. Chứng minh tam giác ABC đều và tính độ dài cạnh của tam giác. 
d) Gọi E là giao điểm của OA với cung nhỏ BC. Chứng minh E là tâm đường tròn nội 
tiếp tam giác ABC. 
d) Vẽ cát tuyến AMN, I là trung điểm của MN. Chứng minh 5 điểm A, B, O, I, C cùng 
nằm trên một đường tròn. 
e) Chứng minh AM.AN = AB2. 
Bài 2. Cho đường tròn (O) đường kính AB = 2R. Vẽ các tiếp tuyến Ax và By (Ax, By cùng 
thuộc nửa mặt phẳng bờ AB). Qua điểm M trên (O) (M khác A và B) vẽ đường thẳng vuông 
góc với OM cắt Ax, By lần lượt tại C và D. 
a) Chứng minh CD là tiếp tuyến của đường tròn (O). 
b) Chứng minh A, C, M, O cùng thuộc một đường tròn. 
c) Chứng minh AC + BD = CD và 0COD 90 
d) Chứng minh AC.BD = R2 và 
2 2
1 1
OC OD
 không đổi. 
e) Xác định vị trí của M để CD có độ dài nhỏ nhất. 
Bài 3. Cho đường tròn (O; R) đường kính AC. Trên đoạn thẳng OC lấy điểm B và vẽ đường 
tròn (O’) đường kính BC. Gọi M là trung điểm của AB. Qua M kẻ dây DE của đường tròn (O) 
vuông góc với AB. CD cắt đường tròn (O’) tại I. 
a) Tứ giác DAEB là hình gì? Vì sao? 
b) Chứng minh MI là tiếp tuyến của đường tròn (O’). 
c) Gọi H là hình chiếu của I trên AC. Chứng minh MH.MO’ = MA.MC. 
Bài 4. Cho ABC vuông tại A. Gọi O là tâm đường tròn ngoại tiếp ABC, d là tiếp tuyến 
của đường tròn tại A. Các tiếp tuyến của đường tròn tại B và C cắt d tại D và E. Chứng minh: 
 a) Góc DOE vuông. b) DE = BD + CE 
 c) BC là tiếp tuyến của đường tròn đường kính DE. 
Bài 5. Cho (O; R), dây BC khác đường kính. Qua O kẻ đường vuông góc với BC tại I, cắt 
tiếp tuyến tại B của đường tròn ở điểm A, vẽ đường kính BD. 
 a) Chứng minh CD // OA. 
 b) Chứng minh AC là tiếp tuyến của đường tròn (O). 
 c) Đường thẳng vuông góc BD tại O cắt BC tại K. Chứng minh IK.IC + OI.IA = R2. 
(Xem lại các bài tập 41, 42, 43 SGK trang 128) 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 9 
CÁC ĐỀ TỰ LUYỆN 
Đề 1 
Bài 1 (1,0 điểm): Thực hiện phép tính: 
a) 2 3. 2 3 b) 
15 3 2
1 5 3 1
Bài 2 (2,0 điểm): Cho 
1 1 x
A : x 0, x 9
x 9x 3 x 3
a) Rút gọn A b) Tìm MaxB biết B A x x 
Bài 3 (3 điểm): Cho (d1): y = – x + 2 và (d2): 
1
y x 2
3
1) Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ. 
2) Tìm tọa độ giao điểm A của (d1) và (d2). 
3) Tính góc tạo bởi (d2) với trục Ox (làm tròn đến phút). 
4) Tìm m để ba đường thẳng (d1), (d2) và (d3) y = (1 – 3m)x + 2 đồng quy. 
Bài 4 (4,0 điểm): Cho tam giác ABO vuông tại B, OB = a, OA = 2a. 
1) Giải tam giác vuông OAB. 
2) Vẽ đường tròn (O; OB). Từ A vẽ tiếp tuyến AC của (O) (C là tiếp điểm, C khác B). 
a) Chứng minh OA  BC tại H (H là giao điểm của AO và BC). 
b) Đoạn thẳng OA cắt (O) tại M. Chứng minh M là tâm đường tròn nội tiếp ∆ABC. 
c) Đường thẳng vuông góc với OB tại O cắt AC tại N và cắt BC tại I. Chứng minh 
MN là tiếp tuyến của đường tròn (O) và HI.HB + HM.HA = a2. 
Đề 2 
Bài 1 (1,0 điểm): Thực hiện phép tính: 
a) 2 2 3 361 60 64. 125 196 : 49 b) 
2
75 2 3 
Bài 2 (1,5 điểm): Giải các phương trình 
 a) x 4 x 4 4 b) 
x 3
9x 27 1
4
Bài 3 (3,5 điểm): Cho hàm số bậc nhất y = (3 – 2m)x + m – 1 
1) Tìm m để hàm số đồng biến trên . 
2) Với m = 2, vẽ đồ thị hàm số trên, tính diện tích của tam giác tạo bởi đồ thị hàm số với 
hai trục tọa độ. 
3) Tìm m để đồ thị hàm số song song với đường thẳng y = 2x. 
4) Tìm m để đồ thị hàm số cắt đường thẳng y = x – 2 tại một điểm trên trục hoành. 
5) Chứng minh đồ thị hàm số y = (3 – 2m)x + m – 1 luôn đi qua một điểm cố định. 
Bài 3 (1,5 điểm): Giải tam giác ABC vuông tại A có AB = 5 cm, 0B 30 
Bài 4 (2,5 điểm): Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn (O) vẽ tiếp tuyến 
AB (B là tiếp điểm). Vẽ dây BC vuông góc với OA tại H. 
a) Chứng minh AC là tiếp tuyến của (O). 
b) Với OA = 2R. Chứng minh tam giác ABC đều. 
c) Trên tia đối của tia BC lấy điểm M. Từ M vẽ hai tiếp tuyến MD và ME của đường tròn 
(O) (D và E là các tiếp điểm). Chứng minh ba điểm A, D, E thẳng hàng. 
TRƯỜNG THCS HUNG THANG
 ĐỀ CƯƠNG ÔN TẬP HK I – TOÁN 9 
 Trang 10 
Đề 3 
Bài 1 (3 điểm): 
1) Thực hiện phép tính: 8 3 32 72 
2) Giải phương trình: 2x 6x 9 8 
3) Rút gọn biểu thức: 
x 1 2 x 2 5 x
A
4 xx 2 x 2
 rồi tìm x để A < 1. 
Bài 2 (3 điểm): Cho hai hàm số y = 0,5x + 1 (d) và y = -2x + 4 (d’) 
1) Vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ. 
2) Gọi E là giao điểm của (d) và (d’). Tìm tọa độ giao điểm E. 
3) Tìm m để đồ thị hàm số y = (m - 3)x + 2 và đường thẳng (d) vuông góc nhau. 
Bài 3 (1,5 điểm): Cho tam giác ABC vuông tại A, biết AB = 6cm, BC = 8cm. 
1) Giải tam giác vuông ABC. 
2) Tính độ dài đường cao AH, đường phân giác AD. 
Bài 4 (2,5 điểm): Cho nửa đường tròn tâm O, đường kính AB, kẻ hai tiếp tuyến Ax, By (Ax, 
By thuộc cùng một nửa mặt phẳng bờ AB). Gọi C là một điểm trên tia Ax, kẻ tiếp tuyến CM 
với nửa đường tròn (M là tiếp điểm), CM cắt By ở D. 
1) Tính số đo góc COD và chứng minh tích AC. BD không đổi khi C di chuyển trên Ax. 
2) Gọi I là giao điểm OC và AM, K là giao điểm của OD và MB. Tứ giác OIMK là hình 
gì? Vì sao? Chứng minh AB là tiếp tuyến của đường tròn đường kính CD. 
3) Gọi N là giao điểm của AD và BC. Tia MN cắt AB tại H. Chứng minh N là trung điểm 
của MH. 
Đề 4 
Bài 1 (3 điểm): 
1) Thực hiện phép tính: a) 2 8 50 b) 1 1
3 2 3 2
 c) 8 2 15 5 
2) Cho biểu thức : P = 
a 4 a 4 4 a
a 2 2 a
 ( Với a 0 ; a 4 ) 
a) Rút gọn biểu thức P. b) Tìm giá trị của a sao cho P = a + 1. 
Bài 2 (3 điểm): Cho hàm số y = (1 – a)x + 3 (d) 
1) Xác định a biết (d) đi qua A(1; -2). Vẽ đồ thị với a vừa tìm được.. 
2) Xác định a biết đường thẳng (d) song song với đường thẳng y = 2x – 1 (d’) 
3) Tìm tọa độ giao điểm B của (d) và (d’) với a tìm được ở câu a bằng phép tính. 
4) Tìm m để A, B, C(2; 1 – 2m) thẳng hàng. 
Bài 3 (1,5 điểm): Cho MNP vuông tại M có MN = 10cm, 
0P 50 . 
Bài 4 (2,5 điểm): Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại A. Kẻ tiếp 
tuyến chung ngoài DE, D (O), E (O’) (D, E là các tiếp điểm). Kẻ tiếp tuyến chung trong tại 
A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. 
1) Chứng minh I là trung điểm của DE. 
2) Chứng minh tứ giác AMIN là hình chữ nhật.Từ đó suy ra hệ thức IM. IO = IN.IO’. 
3) Chứng minh OO’ là tiếp tuyến của đường tròn đường kính DE. 
4) Chứng minh DE 2 R.R ' . 
TRƯỜNG THCS HUNG THANG